Matematik herhangi bir fiziksel araç kullanılarak doğrudan ölçülemeyen çoklukları belirlemeye adanmış bir nicelik bilimi olarak ortaya çıkmıştır. Başlangıçta iki ana dal; aritmetik (kesikli miktarların incelenmesi) ve geometri (sürekli miktarların incelenmesi) olmasına rağmen tarihsel süreç içerisinde matematiğin bu tanımı terk edilmiş ve büyüklüklerin ölçümü ile belirgin bir ilişkisi olmayan yeni matematik dalları geliştirilmiştir. Günümüzde matematik dendiğinde gerekli sonuçlara varılan bir bilim anlaşılmaktadır.
Matematikçinin varoluşunun ana nedeni problem çözmektir. Aniden eski bir sırrı öğrenmenin ya da yeni bir gerçeği keşfetmenin hazzı; aydınlanma, neredeyse inanılmaz derecede gelişmiş bir bakış açısı, coşku ve yerinde duramama parıltısına sahiptir. Her anlamlı yaşamın büyük kısmı, teknisyenlerin, mühendislerin, bilim adamlarının vb. mesleki yaşamının önemli bir kısmı, matematiksel problemlerin çözümünden oluşmaktadır. Matematiksel problemler, hala büyüyen ve çiçek açan oldukça geniş bir literatüre sahiptir.
Matematik yapmanın en güçlü motivasyonu; gurur, zafer hissi ve zor bir problemi çözmenin memnuniyetidir. Matematiksel problemleri çözmek için gereken araştırmalar uzun süren aralıksız bir çalışmayı gerektirebilir. Peki matematiği nasıl yapabiliriz?
Bu soruyu cevaplamak için matematiğin içeriğinin ne olduğunu bilmemiz gerekmektedir. Matematik; tanımlar, semboller, formüller, teoremler, ispatlar ve yöntemler olmadan düşünülemez. Bunlar çoğu matematikçinin sözlüğünde var olan saygın kelimelerdir ve mantıksal yanlışlıktan kaçınarak matematiğin yazılmasına izin veren matematiksel titizliği yani matematiğin ilk bileşenlerini oluşturmaktadırlar. Bu ise, hiçbir şeyin ispat denetimi sorumluluğu nedeniyle örtülü bırakılamamasını ve tüm varsayımların doğru bir şekilde belirtilmesini gerektirmektedir.
Güçlü bir önsezi matematiğin önemli bir bileşenidir. Bu, matematiksel kavramların derinlemesine anlaşılmasını ve matematiksel yapıların canlı nesneler gibi ele alınmasını gerektirmektedir. Sezgi, yeni keşiflere yol açabilecek derin kavrayışların yansımasıdır. Sezgisel düşünme, matematikçiler için genellikle semboller yerine kelimeler ve rakamlar kullanılmasıdır.
Eğer, önsezileriniz doğru ise, onları detaylı kanıtlara dönüştürmek kolay olmalıdır. İşte size bir örnek;
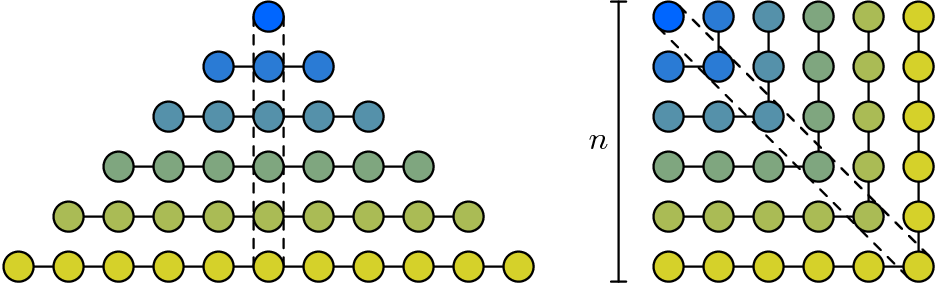
Şekil: İlk n tek doğal sayıların toplamı
Şimdi, hırslı bir matematikçi kalemini alıp yukarıdaki resmi n2’dir(1)
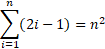
ifadesi için kesin kanıt veren bir denklem zincirine dönüştürecektir ya da gözlerini kapatıp yaslandığı sandalyesinde bu denklemleri kafasının içinde görmeyi tercih edecektir.
Kimler Matematik Bölümünü Tercih Etmelidir?
Analitik düşünebilen
'(1) AoPS Online: https://artofproblemsolving.com/wiki/index.php/Proofs_without_words#note_1