Mathematics started as the science of quantity; a science devoted to determining quantities that cannot be measured directly using any physical tool. There were two main branches: arithmetic (the study of discrete quantities) and geometry (the study of continuous quantities). Throughout the history, this description of mathematics was abandoned, and new branches of mathematics which bore no obvious relation to measurement of quantities were developed. Nowadays, mathematics is understood to be the science that draws necessary conclusions.
The mathematician’s main reason for existence is to solve problems. The joy of learning a former secret – as same as the joy of discovering a new truth – has the flash of enlightenment, the incredible enhanced vision, and the elation and euphoria of released tension. The major part of every meaningful life is the solution of problems; a considerable part of the professional life of technicians, engineers, scientists, etc., is the solution of mathematical problem. Mathematical problems have quite an extensive literature, which is still growing and flowering.
The strongest motivation of doing mathematics is the pride, the feeling of victory, the almost malicious satisfaction of solving a hard problem. The research required to solve mathematical problems may take long time of sustained inquiry. But how can we do mathematics?
To answer this question, we need to know what the ingredients of mathematics are. Mathematics could surely not exist without definitions, symbols, formulas, theorems, proofs and methods. These are respected words in the vocabulary of most mathematicians, and they form the first ingredient of mathematics, namely the mathematical rigour, which allows to write mathematics avoiding logical fallacy. It requires all assumptions to be properly stated; nothing can be left implicit, with the amenability to essential algorithmic proof checking.
An important ingredient of mathematics is strong intuition. That requires a deep understanding of the mathematical concepts and dealing with mathematical structures as living objects. The intuition is the reflection of the deep insights that may lead to new discoveries. For intuitive thinking, mathematicians usually use words and figures, rather than symbols. But it should be an easy task to convert the intuition into rigorous proofs, otherwise the intuition is false. Here is an example:
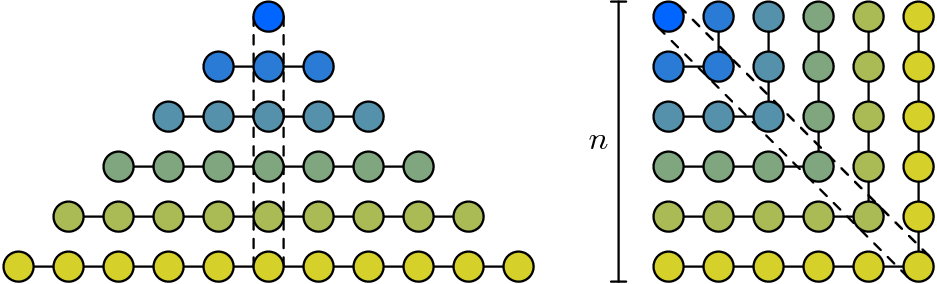
Figure: The sum of the first n odd natural numbers is n2.1
Now, an ambitious mathematician will pick up his pencil and convert the above picture into a chain of equations that gives a rigorous proof for the fact that i=1n(2i-1)=n2, or, if she/he prefers, she/he may lean back in his chair, close her/his eyes, and look at those equations inside her/his head.
(1) AoPS Online: https://artofproblemsolving.com/wiki/index.php/Proofs_without_words#note_1
Who Should Prefer Mathematics Department?